

二進数と十進数のちがい

二進数を十進数に変換する方法、十進数を二進数に変換する方法の解説と変換テスト問題です。
0と1だけで数値を表すのが2進数
0,1,2,3,4,5,6,7,8,9 と10種類の文字を使って数値を表すのが10進数。
0と1だけの2種類の文字で数値を表すのが2進数です。
コンピューターの内部では、「電圧が高い」か「電圧が低い」かの二種類で状態を判別するので、二進数が使われています。
2進数では、0の次は1(これは10進数と同じ)。
で、1の次は、ケタが上がって10となります(十進数だと「2」)。
あとは、この繰り返し。
2進数で、10の次は11。その次は桁が上がって100です。
十進数の1から10までを二進数にするとこんな感じ(↓)。
| 十進数 | 二進数 |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
十進数から二進数への変換方法
十進数を二進数に変換するには、2で割り続けて、「あまり」を並べます。
「13」を2進数に変換する場合で説明します。。
まず、13を2で割ると答えは、6あまり1。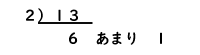
つぎに、6を2で割ると答えは、3あまり0。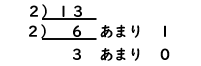
さらに、3を2で割ると答えは、1あまり1。
答えが1になったら終わり。
左下から、右上に向かって、1と0を並べると二進数になります。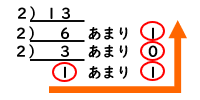
「13」の2進数は、1101
二進数から十進数への変換方法
2進数を10進数に変換するには、ケタごとの2のn乗を足していきます。
「110101」を十進数に変換する場合で説明します。
まず、2進数下1ケタ目を2の0乗、下2ケタ目を2の1乗…として計算します。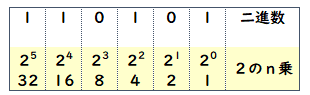
2進数で「1」となっているケタの累乗の数字を書き出します。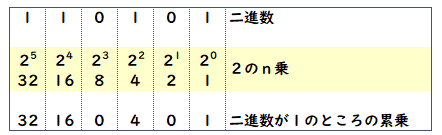
書き出した数字を足したのが、変換した十進数です。
32+16+4+1=53
110101の十進数は、53
二進数、十進数変換の確認テスト問題
習うより慣れろ。
理屈より解いてみよう。
問題:次の数値を2進数または10進数に変換せよ。
(2進数に変換せよ)となっている数字は10進数、
(10進数に変換せよ)となっている数字は2進数です。
| 問題 | 解答 |
|---|---|
| 72(二進数に変換せよ) | 1001000 |
| 81(二進数に変換せよ) | 1010001 |
| 99(二進数に変換せよ) | 1100011 |
| 110110(十進数に変換せよ) | 54 |
| 111111(十進数に変換せよ) | 63 |
赤い部分をクリックすると正解が表示されます。
別の問題で再チャレンジ
何回も挑戦してみてください。



